Eine Option, wenn Sie hauptsächlich an der Darstellung der einzelnen Ziffern von pi interessiert sind, besteht darin, eine Darstellung in einer anderen Basis als 10 zu verwenden. Beispielsweise hätte pi Basis 12 für jede Chromatik ein individuelles Digital Hinweis:

Hier ist eine Website, die Ihnen den Einstieg erleichtern kann: http://www.virtuescience.com/pi-in-other-bases.html

Die Zahl 10 passt nicht unbedingt gut zu Werten in der traditionellen Musiktheorie. (Zum Beispiel gibt es 12 chromatische Tonhöhen pro Oktave unter Verwendung herkömmlicher Oktavunterteilungen; diatonische Skalen haben sieben Tonhöhen; die Dauer der Noten bezieht sich auf Potenzen oder negative Potenzen von 2). Aus diesem Grund ist die Welt Ihre Auster! Ich denke, Sie können beliebige 10 Werte auswählen, um sie den 10 Ziffern zuzuordnen.

Dies bedeutet, dass Sie wahrscheinlich keine endgültige Antwort erhalten (und daher können einige diesen Beitrag in Betracht ziehen nicht zum Thema gehören), aber hier sind einige meiner eigenen Vorschläge für geeignete Zuordnungen:

1. Teilen Sie eine Oktave durch zehn (dh verwenden Sie 10-TET), obwohl dieses Youtube Der Clip deutet darauf hin, dass Sie jemand geschlagen hat…!
2. Verwenden Sie 10 verschiedene Akkorde.
3. Verwenden Sie 10 verschiedene Notendauern (die entweder durch Potenzen von 2 oder als Zehntel von in Beziehung gesetzt werden können ein bestimmter Wert).
4. Verwenden Sie ein Paar ineinandergreifender pentatonischer Skalen (Ich mag diese Idee, vielleicht in Stereo getrennt, aber es ist nicht mein Projekt…)
5. Verwenden Sie eine Kombination der oben genannten Ideen , z.B. Unterschiedliche Frequenzen haben jeweils auch ihre eigene Dauer (und Stereopositionierung…).
ol>

Am Ende kam ich sehr schnell auf diese Ideen, die Möglichkeiten sind riesig und Experimentieren ist der Schlüssel.

ZUSÄTZLICHE INFORMATIONEN: Wenn Sie versuchen, die Frequenzen bei der 10-TET-Abstimmung zu finden, multiplizieren Sie eine Startfrequenz mit 2 mit der Potenz von n / 10, wobei n eine ganze Zahl ist Werte im Bereich von 0 bis 9.

Pi kann auch durch verschiedene unendliche Reihen ausgedrückt werden. Ich mag die 1593 entdeckte François Viète-Serie:

Quadratwurzel von 2 ist eine halbe Oktave entfernt. Vielleicht ist es möglich, die Serie als eine Folge von Klängen darzustellen? Oder passt vielleicht eine andere Serie besser? Dies könnte den Geist von Pi noch besser reproduzieren als die Wiedergabe seiner Dezimaldarstellung.

Eine Idee, die ich nicht erwähnt habe, ist Rhythmus. Vielleicht können Sie einige der Ersatzziffern als Tempowechsel verwenden (z. B. von acht zu acht wechseln). Oder Sie können die Ersatzziffern vorgefertigten rhythmischen Motiven zuordnen.

Eine andere Idee wäre, die Ziffern, die keiner Note zugeordnet sind, zum Wechseln des Instruments zu verwenden.

HTH.

Warum Base 10 verwenden? Sie müssen irgendwo einen Kompromiss eingehen, und da π bereits transzendent ist, gibt es keinen rationalen Radix, der π genau darstellt. Wenn Sie heptary verwenden, π ≈ 3.0663651432036134110263402244652226643520650240155443215426431025161154565220002622436103301443233631 . Diese Ziffern passen perfekt zu den sieben Tonhöhen in einer Oktave. Die Verwendung von Oktal würde entweder a b3 , b7 oder # 4 hinzufügen. Quintary würde eine perfekte pentatonische Skala ergeben.

Wenn Sie ein schönes Musikstück machen möchten (was ich vermute, würde es ein wenig verschwenderisch erscheinen, pi einfach zu codieren), würde ich es vermeiden, die Musik mechanisch zu generieren, und stattdessen Pi-Stücke als Inspiration verwenden.

Zum Beispiel:

• Schreiben in 22/7 (eine Annäherung an pi)
• Verwenden der ersten 5 oder so Ziffern als Motiv in irgendwie und mit den anderen nicht so oft. Sie könnten dann weitere 50 Ziffern als schnellen Abschnitt vom Typ Kadenz haben.
• Verwenden von zyklischen Akkordfolgen (pi handelt von Kreisen)

Eine Option, die niemand wirklich erwähnt hat, besteht darin, diese zusätzlichen Ziffern für spezielle Zwecke zu verwenden (z. B. Tempo ändern, ein anderes Instrument). Wenn das Hauptinstrument ein Klavier ist, würde ich mir vorstellen, dass das einfache Zuweisen einer Ziffer zu Snare, Bass und Becken Ihrer endgültigen Musik viel Flair verleiht.

Tatsächlich wird das Hinzufügen neuer Instrumente geöffnet Sie haben eine Reihe neuer Möglichkeiten, dies zu tun. Sie können jede Ziffer eine Operation darstellen lassen. Jede Operation könnte ein Instrument, ein Tempo oder eine Effektänderung usw. darstellen. Außerdem würde jede Operation dann so viele Ziffern einlesen, wie sie benötigt, um die Parameteranzahl zu erfüllen. Auf diese Weise können Ihre Beats Dinge wie Sustain, Akzent usw. für Ihre Notizen haben.

Dadurch wird das Problem, mehr Datenraum als Notenraum zu haben, noch problematischer die Tatsache, dass es anfangs nie wirklich ein Problem war. Füllen Sie einfach den zusätzlichen Raum mit den nächsthöheren und niedrigeren Oktaven auf. Dies führt zu einem leichten Ungleichgewicht der Noten, aber wir wollen sowieso kein Gleichgewicht ...

Was uns zu einem anderen Problem führt. Ich denke, Ihre beste Wahl ist es, Muster zu verwenden, die in der populären Musik zu finden sind, um sicherzustellen, dass Ihre Notenverteilung angenehm ist. Ich habe diese Site gefunden, die die Daten enthält, die wir benötigen würden, um Folgendes festzustellen:

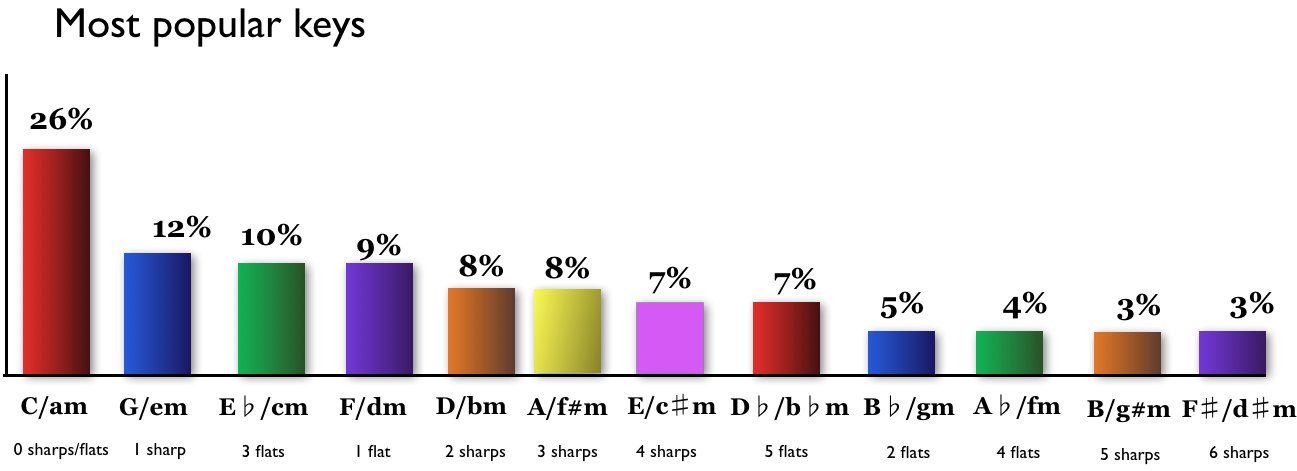
Ihre Anwendung wird mit größerer Wahrscheinlichkeit besser klingen, wenn es erzeugt Noten mit einem ähnlichen Dispersionsmuster wie dieses. Sie werden vielleicht feststellen, dass einige Instrumente sehr unterschiedlich funktionieren, daher ist das Experimentieren (wie bei all dem) wichtig.

Sobald dieses System funktioniert, würde ich vorschlagen, sich ein anderes Lied auszudenken, das es ist klingt ähnlich wie das, was Sie haben, und macht ein genaueres Diagramm zur Notenverteilung, das tatsächlich zu einem Song in derselben Tonart passt. Lesen Sie die Seite unter dem obigen Link, um zu sehen, was ich meine.

Wenn Sie noch einen Schritt weiter gehen möchten, können Sie so viele Funktionen hinzufügen, wie Sie möchten. Sie müssen nur entscheiden, wie groß ein Op-Code ist (1,2,3 Zeichen), abhängig davon, wie viele verschiedene Funktionen Sie haben, und sie alle handhaben (auch wenn große Blöcke dasselbe tun). Wenn Sie wirklich möchten, dass dies eine komplexe Symphonie ist, würde ich vorschlagen, dass Sie den Verarbeitungsschritt vom Wiedergabeschritt trennen, um alle Zeitprobleme zu beseitigen, die Sie aufgrund der variablen Datenrate haben, die einem solchen Design inhärent ist. Zum Glück gibt es Standards. Ein beliebter Standard heißt MusicXML. Wenn Sie Ihr Programm so gestalten, dass diese Dateien einfach generiert werden. Anschließend können Sie diese Dateien später mit einem MusicXML-Player wiedergeben.

Update: Wenn Sie meine Experimente damit sehen möchten, erhalten Sie diese möglicherweise sie hier.

Es gibt keinen Grund, innerhalb einer Oktave zu bleiben. Sie können beispielsweise C-D-E-F-G-A-B-c-d-e für Ihre Ziffern verwenden. Die ersten fünf Noten sind also beispielsweise E-C-F-C-G-d. Dies hat den Vorteil, dass es für jeden Musiker äußerst intuitiv ist, da Sie sich nur auf Skalengrade in C-Dur beziehen (wobei 10 0 ist). Ich persönlich kann einfach da sitzen und die Noten lesen und spielen, ohne darüber nachzudenken.

Mit der Moll-Tonart, die Sie verwenden, können Sie auch die Dur-Tonart ausleihen, ua die harmonische Moll-Tonart. Dann könnten Sie A-B-C-D-E-F-F # -G-G # -a verwenden. Dies ist nicht so intuitiv, erzeugt jedoch einige interessante Effekte, ohne vollständig chromatisch zu wirken. Die ersten paar Noten werden zu C-A-D-A-E-G # -B-F-E-C-E G-G # -F # -G # -C-B-C-G-D-F B-F-D-C-C-G-C-B-F # -G # -E-a. Das letzte Bit klingt nach einer tatsächlichen Trittfrequenz.

Als Programmierer liebe ich diese Idee und natürlich habe ich auch schon darüber nachgedacht, aber noch keine Zeit gehabt, dies auszuprobieren :).

Grundsätzlich glaube ich Ihrer Linie mit Notizen ist falsch. Sie sollten zunächst einen Schlüssel auswählen, in den Sie ihn schreiben möchten. Ich glaube, Ihr Schlüssel wäre Am, oder ist es ein Zufall? Ich würde mit so etwas arbeiten:

 char notes [] = {'A', 'B', 'C', 'D', 'E', 'F', 'G'}; String pi = String.valueOf (Math.PI); für (int i = 0; i < pi.length (); i ++) {char currentChar = pi.charAt (i); if (currentChar! = '.') {// negiere das Dezimal-Didigt System.out.println (currentChar); char currentNote = notes [(Integer.parseInt (currentChar + "") - 1)% notes.length]; System.out.println (currentNote); }} 

Beachten Sie, dass dies Java ist.

BEARBEITEN: Dieser Code ist so konzipiert, dass Sie eine Nummer haben, die größer ist als die Anzahl der bereitgestellten Notizen beginnt wieder mit der ersten Note. 8 wäre also die Note 0 (A) zurück.

Andere Antworten haben vorgeschlagen, andere Grundlagen zu verwenden. Für eine Veranstaltung in der Abteilung Physik habe ich Pi in Quintal gespielt, und es gibt ein Video. Das Blatt wurde mit einem Skript und Lilypond erstellt.

Bonus: auch in Oktal, aber dieses ist nicht kommentiert.

Hier ist eine andere Idee, die selbst nach meinen Maßstäben bizarr ist. Für diejenigen, die mit der 12-Ton-Kompositionsregel nicht vertraut sind (wie ursprünglich angegeben; wahrscheinlich viele Male geändert), heißt es, dass Sie keinen Ton wiederholen können, bis die anderen 11 gespielt wurden. Seriell oder in Akkorden ist zulässig.

Hier ist also die Kompositionsregel "12-Ton-Pi": Für jede Ziffer von Pi dürfen Sie im nächsten 12-Zyklus so viele Töne überspringen. Zum Beispiel benötigt der erste Zyklus nur 9 (12-3) Töne, bevor er wiederholt wird; Der nächste Zyklus benötigt 11 (12-1) Töne und so weiter.

Bonuspunkte, wenn Sie das Stück NICHT wie Webern oder Berio klingen lassen können :-)